К ТЕОРИИ УДАРНОЙ АКТИВАЦИИ ЦЕМЕНТНОЙ СМЕСИ. ЧАСТЬ 1. ВЛИЯНИЕ НА ПРОЧНОСТЬ БЕТОНА

Категория: Строительство. Архитектура.

Важное место среди новых высокоэффективных строительных материалов XXI в. занимают мелко- и тонкозернистые бетоны. Чем меньше зерна новообразований и размеры пор между ними, тем выше прочность бетона даже при одном и том же водоцементном отношении [1]. Получению тонкодисперсной структуры в значительной мере способствует механоактивация цемента, инертных материалов и сырьевых смесей [2]. Ее положительное действие связано не только с повышением удельной поверхности твердых дисперсных фаз, но и с ростом дефектности их частиц, то есть с переходом в неравновесное состояние. Клинкерные частицы с дефектами находятся в состоянии с более высокой поверхностной энергией, что повышает их гидратационную активность [3].

Теоретически и экспериментально установлено, что наиболее эффективным способом механической активации при измельчении частиц цемента является ударное воздействие [4, 5]. Поэтому для ее проведения необходимо применять помольные агрегаты, в которых осуществляется принцип разрушения твердого материала свободным ударом [6]. Такими агрегатами являются дезинтеграторы, планетарные и роторно-вихревые мельницы, пневматические активаторы, электромагнитные аппараты вихревого слоя и т. п.

Обработка цементного теста (при В/Ц = 1 : 1) потоком игольчатых ферромагнитных частиц металла, движущихся под действием внешнего вращающегося магнитного поля в аппарате вихревого слоя, приводит к увеличению активности цемента [7] и прочности цементно-песчаного раствора [8]. На рисунке 1 представлена полученная в работе [8] зависимость предела прочности Rсж на сжатие образцов из цементно-песчаного раствора после 28 сут твердения от времени активации. Одновременно с этим происходит измельчение частиц цемента, и таким образом растет его удельная поверхность Sуд [7, 8].

Связь между Rсж и Sуд экспериментально исследована [9]. Чем больше удельная поверхность частиц цемента, тем больше его реакционная способность, тем больше интенсивность гидратации, и поэтому больше ранняя прочность цементного камня. По разным литературным данным, зависимость Rсж от Sуд близка к линейной в интервале значений Sуд = 2500…5000 см2/г. На рисунке 2 представлена зависимость прочности цементного камня в возрасте 28 сут от удельной поверхности цемента, используемого для цементации оснований гидротехнических сооружений [9].

Целью данной работы является разработка теоретической модели, описывающей влияние активации цемента на прочность. Пусть

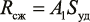,(1)

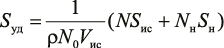.(2)

Здесь N0 – начальное число исходных частиц цемента объемом Vис и площадью поверхности Sис, N – число исходных частиц цемента на момент времени t, Nн – число новых частиц цемента объемом Vн и площадью поверхности Vн после измельчения исходных частиц на момент времени t, ρ – плотность цемента.

Очевидно, что быстрота изменения количества исходных частиц N пропорциональна их количеству:

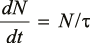,(3)

Это приводит к интегральному соотношению

.(4)

На рисунке 3 представлена зависимость относительного числа исходных частиц цемента N/N0 от времени измельчения при τ = 40 с. Число раздробленных исходных частиц N0 – N:

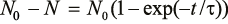.(5)

Число новых частиц Nн меньшего размера связано с числом раздробленных исходных частиц следующим образом:

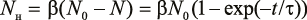,(6)

Выражение (6) приводит к соотношению (7):

Vис = βVн,(7)

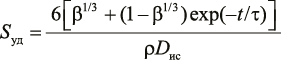.(8)

Учитывая в (1) соотношение (8), можно описать релаксационное поведение предела прочности бетона Rсж(t) выражением

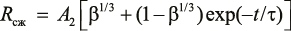.(9)

Здесь A2 – коэффициент пропорциональности.

На рисунке 1 сплошная линия представляет теоретический результат, полученный по формуле (9) при ρ = 2 · 103 кг/м3, Dис = 10–5 м, τ = 40 с, β = 2,7, А2 = 47 МПа.

В соответствии с кинетической концепцией прочности твердых тел [10] величину τ – время релаксации разрушения или долговечности частиц цемента размером Dис можно описать формулой

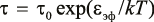.(10)

Здесь τ0 – время распространения механического возбуждения в конденсированной среде, которое можно оценить с помощью соотношения 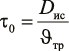(11).

,(11)

В выражении (10) εэф – эффективная энергия связи между атомами.

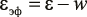.(12)

Здесь ε ∼ 1 эВ – энергия связи между атомами в окислах; w – изменение потенциальной энергии взаимодействия атомов из-за локального ударного взаимодействия частиц при столкновениях, которое можно оценить с помощью соотношения

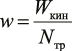.(13)

В выражении (13) 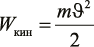– кинетическая энергия одной частицы цемента; ϑ – скорость частицы цемента относительно игольчатых металлических частиц в активаторе; m – масса частицы цемента (~10–12 кг); 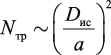– число связей в области трещины (~1010); a – расстояние между атомами в оксидах (~4 · 10–10 м).

С учетом введенных параметров величину времени релаксации (τ = 40 с при Т = 300 К), которая соответствует эксперименту (рис. 1), удается получить, если εэф ∼ 0,7 эВ, Wкин ∼ 10–9 Дж, ϑ ∼ 30 м/с, что согласуется с результатами работы [11]. При вращении игольчатых металлических частиц под действием внешнего переменного магнитного поля с частотой f = 50 Гц необходимая величина относительной скорости (~30 м/с) может быть получена, когда радиус траектории составляет ~0,1 м, что также соответствует экспериментальным данным.

Выводы

Ударная дезинтеграция частиц цемента, приводящая к увеличению его дисперсности, является релаксационным процессом. Величина удельной поверхности частиц цемента определяется механизмом локальных ударных столкновений, в результате чего кинетическая энергия движущихся игольчатых металлических частиц переходит во внутреннюю потенциальную энергию ограниченного числа атомов в области соударения с частицами цемента.

ЛИТЕРАТУРА

  1. Баженов Ю. М. Пути развития строительного материаловедения: новые бетоны // Технологии бетонов. – 2012. – № 3-4. – С. 39–42.
  2. Евтушенко Е. И. Активационные процессы в технологии строительных материалов // Некоторые элементы структурной динамики. – Белгород : Изд-во БелГТУ, 2003. – 195 с.
  3. Прокопец В. С. Влияние механоактивационного воздействия на активность вяжущих веществ // Строительные материалы. – 2003. – № 9. – С. 28–29.
  4. Кузнецова Т. В., Сулименко Л. М. Механо-активация портландцементных сырьевых смесей // Цемент. – 1985. – № 4. – С. 20–21.
  5. Сулименко Л. М., Майснер Ш. Н. Влияние механоактивации на технологические свойства портландцементных сырьевых смесей // Известия вузов. Химия и химическая технология. – 1986. – Т. 29, № 1. – С. 80–84.
  6. Буренина О. Н., Давыдова Н. Н., Андре-ева А. В., Саввинова М. Е. Влияние способа измельчения на активность ингредиентов бетонной смеси [Электронный ресурс] // Политематический сетевой электронный научный журнал КубГАУ. – 2015. – № 111. – Режим доступа: http://ej.kubagro.ru/2015/07/pdf /70.pdf.
  7. Филонов И. А., Явруян Х. С. Механиче-ская активация портландцемента в аппарате вихревого слоя [Электронный ресурс] // Инженерный вестник Дона. – 2012. – № 3. – Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/969.
  8. Электромагнитная активация цементного теста и пенобетонной смеси / Е. А. Торлина, А. И. Шуйский, Г. А. Ткаченко [и др.] // Вестник МГСУ. – 2012. – № 12. – С. 154–160.
  9. Адамович А. Н., Колтунов Д. В. Цементация оснований гидротехнических сооружений. – Л. : Энергоиздат, 1964. – 412 с.
  10. Журков С. Н. Кинетическая концепция прочности твердых тел // Вестник АН СССР. – 1968. – № 3. – С. 46–52.
  11. Уваров В. А., Шаптала В. Г., Шаптала В. В., Овчинников Д. А. Новое направление механоактивации цемента // Вестник БГТУ. – 2013. – № 3. – С. 68–73.

Метки: Строительство и архитектура