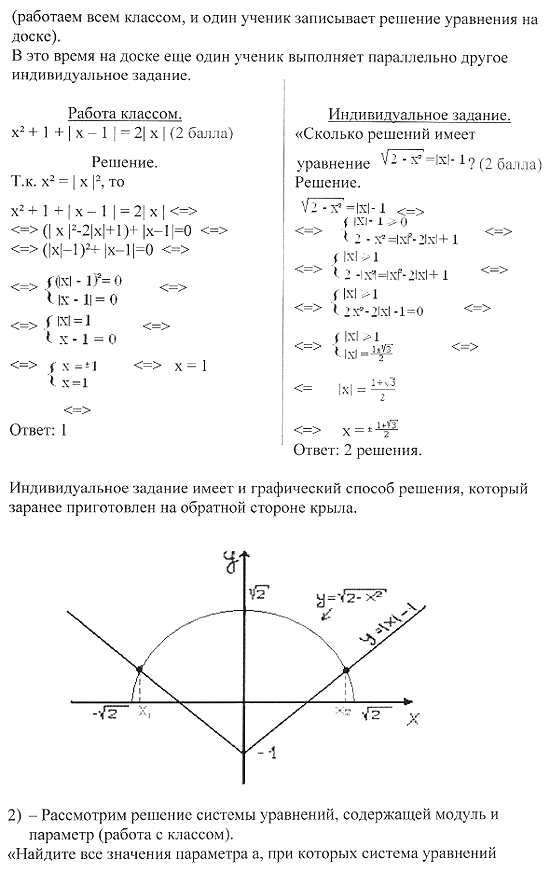
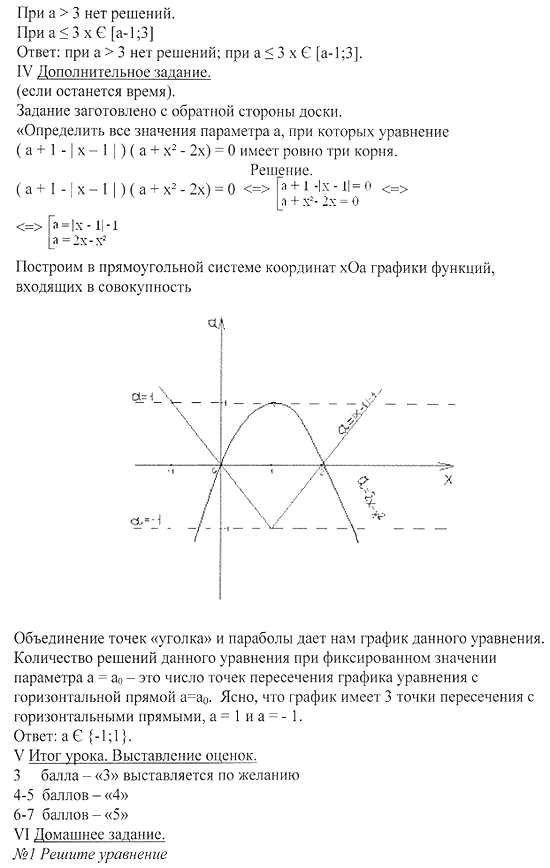
Геометрический способ решения уравнений и неравенств с модулем, 9-й класс

Категория: Математика.

Цель: рассмотреть геометрическое определение модуля. Уметь применять его для решения уравнений и неравенств с модулем, развивать умение исследовать уравнения с параметрами.

Ход урока

1. Организационная часть (Цель занятия)

2. Актуализация знаний

• Алгебраическое определение модуля
  

  |a| =

• Вычислите модули чисел: 3, -8, 10, 0.
• Решите уравнения
  

  |x| = 4	|x| = -4	|x| = 0

• Решите неравенства
  

  |x| > 5	|x|

• Запишите к каждому чертежу соответствующее уравнение или неравенство
  

  

3. Изучение нового материала

• Найдите расстояние между двумя точками координатной прямой
  

  А) А(-1) и В(3)
  Б) Р(0,0001) и Q(132)
  В) М(-2) и N(-87)

• Формула расстояния между двумя точками координатной прямой с координатами х и а: ρ(x,a) = |x - a|

  Геометрическое истолкование выражения |x-a|- это расстояние между двумя точками координатной прямой.

• Отметить на координатной прямой точки, для которых
  

  |x| = 1      |x| ≥ 3      |x| > 2      1 < |x| < 4      |x| = 0      |x| = -1

  

• Каков смысл выражений?
  

  Изобразите множества, задаваемые этими предложениями на координатной прямой. Иными словами переведем аналитические модели на геометрический язык.

  

• Решим неравенство |х-2| <3
  

  Переведем аналитическую модель на геометрический язык: нужно найти на координатной прямой такие точки х, которые удовлетворяют условию ρ (х,2) < 3. Другими словами удалены от точки с координатой 2 на расстояние меньше 3.

  Это все точки, принадлежащие интервалу (-1;5)

  

  Ответ: (-1;5)

• Как решить уравнение?
  

  |х-5|+|х+1|=8

  Выражение |х-5| можно истолковать, как расстояние между точками с координатами х и 5.

  Выражение |х+1| можно истолковать, как расстояние между точками с координатами х и -1.

  Тогда уравнение означает, что нужно найти такую точку Х(х), сумма расстояний от которой до точек с координатами 5 и -1 равна 8.

  Расстояние между точками с координатами 5 и -1 равно 6 < 8, следовательно, точка с координатой х находиться вне отрезка [-1;5] и таких точек две.

  

  Ответ: х=-2, х=6

  Что произойдет, если вместо 8 взять число 1, 6, 100,…? Сколько будет тогда корней уравнения?

  При равенстве суммы модулей 1 – нет решений, так как 1

  При равенстве суммы модулей 6 – множество решений, так как все точки отрезка [-2;6] удовлетворяют условию уравнения.

  При равенстве суммы модулей 100, или любому числу больше 6, уравнение имеет два решения.

  Вывод:

  1. Если сумма модулей больше расстояния между двумя точками, то уравнение имеет два решения.
  2. Если сумма модулей равна расстоянию между двумя точками, то уравнение имеет множество решений, которых принадлежат отрезку между точками.
  3. Если расстояние между двумя точками меньше суммы модулей, то решений нет.

4. Закрепление полученных знаний

• Решите неравенство: |х-5|
  Ответ: (3;7)
• Решите неравенство: |х+3| ≥ 4
  Ответ: x ≤ -7, x ≥ 1
• Решите уравнение: |х-1| +|х+2|=5
  

  

  Ответ: x=2, x=-3

• Изобразите на координатной плоскости решения неравенств:
  

  1. |х-1|+|х+2|=5

  

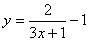
  2. | х-1|+|х+2|<5

  

• Самостоятельно исследуйте, сколько решений может иметь уравнение в зависимости от значений а: |х+3| +|х-1|=

   Ответ:
  а) Если, а=4, то уравнение имеет множество решений – отрезок [-3;1] б) Если а>4, то уравнение имеет 2 корня
  в) Если а

5. Домашнее задание

1. Исследовать уравнение: |х+3| -|х-1|=а

2. Решить № 13, № 16 (а,б)

6. Итог занятия:

• Геометрический смысл модуля
• Как применить геометрический смысл модуля для решения неравенств
• Как применить геометрический смысл модуля для решения уравнений

Литература

1. Мордкович А.Г. Алгебра ,9 класс, в двух частях,6 издание, Москва, Мнеиозина,2004

2. «Метод координат», учебное пособие для учащихся, ОЛ ВЗМШ, Москва ,2002

2.02.2009

• Назад
• Вперед