Готовимся к ЕГЭ по математике. "Задача С. Искусство перевоплощения
Готовясь к ЕГЭ, надо помнить, что задача С6 требует неординарного подхода. Необходимо научиться различным подходам к задаче. Как поэт подбирает слова и образы, чтобы лучше выразить свои мысли и чувства, так и математик подбирает математические модели, которые наиболее удобно и верно отражают сущность поставленной задачи.
Чтобы не быть голословными, разберём два примера, обращая внимание, в первую очередь, на основные принципы, руководствуясь которыми, мы проводим рассуждения.
Пример 1. (Задача 6.4. книга [1])
Найдите все пары натуральных чисел ![]() и
и ![]() , удовлетворяющих равенству
, удовлетворяющих равенству ![]() (в левой части
равенства стоит число, получаемое приписыванием
десятичной записи числа
(в левой части
равенства стоит число, получаемое приписыванием
десятичной записи числа ![]() перед десятичной записью числа
перед десятичной записью числа ![]() ).
).
Решение.
- Применим принцип “особого случая”. Разберём
отдельно крайние значения чисел. Если
 , то
, то  , противоречие.
Если
, противоречие.
Если 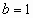 , то
, то  , противоречие.
, противоречие. - Второй шаг. Применим принцип “введения нового
параметра”. Для более полной характеристики
числа
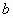 и
удобства записи условия обозначим за
и
удобства записи условия обозначим за  число знаков в
числе
число знаков в
числе 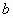 . Тогда
уравнение примет вид:
. Тогда
уравнение примет вид: 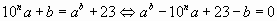 (1).
(1). - Третий шаг. Снова применим принцип “особого
случая”. То есть разберём значение
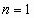 . Уравнение (1) примет вид:
. Уравнение (1) примет вид:  (2). Заметим, что
тогда
(2). Заметим, что
тогда 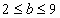 .
. - Четвёртый шаг. Принцип “введения новой
функции”. Будем рассматривать функцию
 при
при  . Причем считаем
теперь переменную
. Причем считаем
теперь переменную 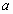 действительным числом. Тогда уравнение
(2) перепишется в виде
действительным числом. Тогда уравнение
(2) перепишется в виде 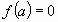 (3).
(3). - Пятый шаг. Применим принцип “функционального
подхода”. А точнее принцип “монотонности”.
Исследуем функцию с помощью производной и найдем
промежутки монотонности. Для этого вычислим
значение функции в крайней точке:
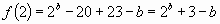 . И производную:
. И производную:  .
. - Шестой шаг. Опять придётся применять принцип
“особого случая”. Рассмотрим отдельно
 . Уравнение (2)
примет вид:
. Уравнение (2)
примет вид: 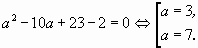
- Седьмой шаг. Вернёмся к принципу
“функционального подхода”. К принципу
“монотонности” добавим принцип
“ограниченности”. Для
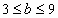 получим
получим 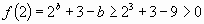 ,
, 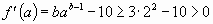 .
Следовательно, функция
.
Следовательно, функция 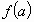 является возрастающей при всех
является возрастающей при всех  , поэтому
, поэтому  и уравнение (3)
не имеет решений.
и уравнение (3)
не имеет решений. - Восьмой шаг. По принципу “полного перебора”
рассмотрим остальные значения
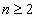 . Тогда
. Тогда 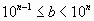 . В этом случае
. В этом случае 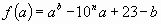 .
. 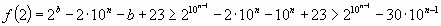 . Снова применим принципы
“введения новой переменной” и “введения новой
функции”. Обозначим для удобства записи
. Снова применим принципы
“введения новой переменной” и “введения новой
функции”. Обозначим для удобства записи  . Введём функцию
. Введём функцию
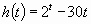 при
при  . Тогда
. Тогда  .
. - Девятый шаг. Повторим принцип “функционального
подхода” к функции
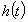 . Вычислим значение функции
. Вычислим значение функции 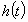 в точке:
в точке:  и производную:
и производную:  .
Следовательно, функция
.
Следовательно, функция 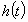 возрастает и
возрастает и 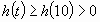 . Тогда получаем неравенство
. Тогда получаем неравенство  .
. - Десятый шаг. Продолжим применять принцип
“ограниченности” к функции
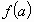 . Вычислим её производную:
. Вычислим её производную:  . Значит,
функция возрастает и
. Значит,
функция возрастает и 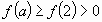
. Поэтому уравнение (3) не имеет решений.
Ответ: ![]() .
.
Другие решения этой задачи можно найти в книгах [1] (с.34) и [2] (с.59).
Пример 1. (Диагностическая работа МИОО, 2010, 10 класс, задача С6)
Натуральные числа ![]() образуют возрастающую арифметическую
прогрессию, причем все они больше 500 и являются
квадратами натуральных чисел. Найдите
наименьшее возможное, при указанных условиях,
значение
образуют возрастающую арифметическую
прогрессию, причем все они больше 500 и являются
квадратами натуральных чисел. Найдите
наименьшее возможное, при указанных условиях,
значение ![]() .
.
Решение.
- Используем принцип “введение правильных
обозначений”. Начнем переводить условие задачи
на язык формул. Во-первых,
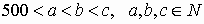 . Во-вторых,
. Во-вторых, 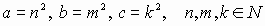 . В-третьих,
. В-третьих, 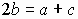 .
. - Тогда получим соотношения:
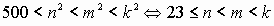 (1);
(1); 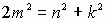 (2). Плохо, что между переменными нет
никакой видимой связи. Попробуем это исправить с
помощью лесенки (то есть обозначать неизвестными
на сколько одна переменная отличается от другой).
Пусть
(2). Плохо, что между переменными нет
никакой видимой связи. Попробуем это исправить с
помощью лесенки (то есть обозначать неизвестными
на сколько одна переменная отличается от другой).
Пусть 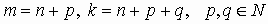 .
. - Преобразуем соотношение (2), используя формулы
сокращенного умножения:
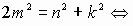
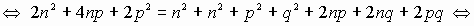
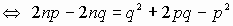 .
Очевидно, что
.
Очевидно, что 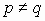 ,
поэтому выразим то, что проще всего (то, что
входит в соотношение линейно):
,
поэтому выразим то, что проще всего (то, что
входит в соотношение линейно):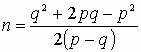 . (3)
. (3) - Снова попробуем улучшить ситуацию с помощью
замены. Упростим знаменатель, обозначив
 . Тогда
. Тогда  . Теперь снова
пересчитаем формулу (3):
. Теперь снова
пересчитаем формулу (3): 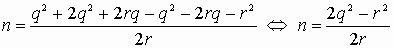 . (4) Из формулы (4) легко следует,
что
. (4) Из формулы (4) легко следует,
что 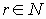 .
. - Займемся теперь рассуждениями на тему
“делимость”. Из (4) следует, что
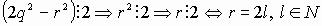 . Подставим
. Подставим 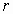 в формулу (4):
в формулу (4): 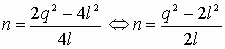 . (5)
. (5) - Повторим процесс (к счастью, он не бесконечен).
Из (5) следует, что
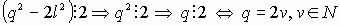 . Подставим
. Подставим 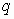 в формулу (5):
в формулу (5): 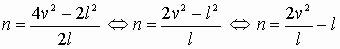 . (6)
. (6) - Подставим полученную формулу (6) в соотношение
(1):
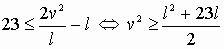 . (7)
Заметим, что нам надо минимизировать значение
. (7)
Заметим, что нам надо минимизировать значение 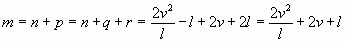 . (8)
. (8)
- Вот теперь можно заняться перебором всех
случаев. Будем менять параметр
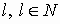 .
. - Первый случай:
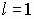 . Тогда
. Тогда 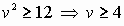 . Из (8) получаем
. Из (8) получаем 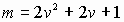 . Наименьшее значение
. Наименьшее значение  принимает при
наименьшем
принимает при
наименьшем 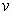 ,
то есть
,
то есть 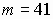 .
. - Второй случай:
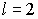 . Тогда
. Тогда 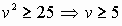 . Из (8) получаем
. Из (8) получаем 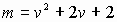 . Наименьшее значение
. Наименьшее значение  принимает при
наименьшем
принимает при
наименьшем 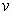 ,
то есть
,
то есть 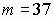 .
. - Третий случай:
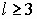 . Тогда
. Тогда 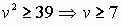 . Следовательно,
. Следовательно, 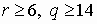 . С учетом ограничения
. С учетом ограничения  , получаем
, получаем  . Поэтому самое
наименьшее значение
. Поэтому самое
наименьшее значение 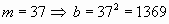
Ответ: ![]() .
.
Примечание. Мы использовали 11 обозначений переменных. Действует правило: чем больше имён, тем меньше вычислений.
Список литературы
- Пратусевич М.Я. и др. ЕГЭ 2011. Математика. Задача С6. Арифметика и алгебра. Под ред. А.Л. Семенова и И.В. Ященко. – М.: МЦНМО, 2011.
- Шевкин А.В., Пукас Ю.О.ЕГЭ. Математика. Задание С6. – М: Издательство “Экзамен”, 2011.
13.07.2012
