Графы и их применение в решении задач
Цель проекта: научиться решать задачи, где требуется пройти по всем мостам так, чтобы побывать на каждом из них только один раз.
Задачи:
- знакомство с задачей о семи кенигсбергских мостах;
- знакомство с математиком Леонард Эйлер;
- научиться рисовать графы, определять четные и нечетные вершины;
- связь между двумя задачами;
- общий метод решения подобных задач.
Этапы работы:
- Определение проблемы.
- Формулировка задач исследования.
- Обсуждение способа построения графа, нахождение четных и нечетных вершин графа.
- Нахождение связи между двумя задачами.
- Самостоятельная работа над проектом.
- Сбор, систематизация и анализ полученных знаний.
- Подготовка к защите проекта.
- Защита проекта.
Основная часть
На математическом кружке я рассказала детям, что через город Калининград (раньше Кенигсберг) протекает река Преголя. Она делится на два рукава и огибает остров. В 18 веке в городе было 7 мостов. Однажды житель города спросил у своего знакомого, сможет ли он пройти по всем мостам так, чтобы на каждом из них побывать только один раз и вернуться к тому месту, откуда началась прогулка. Ребята не смогли пройти по всем мостам один раз и закончить путь там, где он был начат. Тогда я нарисовала еще один мост и поставила точно такой же вопрос. Ребята тратили много времени, но результата не достигли. Тогда я предложила научиться решать такие задачи с помощью графов.
Для этого мы поступили так: “сжали” сушу в точки, а мосты “вытянули” в линии. В результате получили фигуру, которая называется графом.
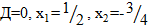
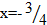
Итак, получили граф. Суши мы обозначили буквами А, B, C, Д (вершины графа). Соединили их линиями. Количество линий равно количеству мостов. Линии, которые соединяют вершины, называются ребрами графа. Мы заметили, что из вершин В, С, Д выходят по 3 ребра, а из вершины А – 5 ребер.
| Кол-во вершин | Кол-во четных вершин | Кол-во нечетных вершин |
| 4 | 0 | 4 |
Все вершины нечетные. Мы не смогли обойти все мосты, побывав на каждом из них один раз.
Попробовали увеличить количество мостов на 1. Их стало 8. Нарисовали граф.
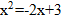
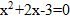
Из вершины Д выходит 4 ребра, из А – 3 ребра, из В – 3 ребра, из С – 3 ребра, из Е – 3 ребра. Одна вершина Д – четная, а четыре вершины – нечетные. Здесь мы тоже не смогли начертить одним росчерком.
| Кол-во вершин | Кол-во четных вершин | Кол-во нечетных вершин |
| 5 | 1 | 4 |
Такой путь долгий и тяжелый.
На следующем занятии я предложила знакомую задачу: Какие буквы русского алфавита можно нарисовать одним росчерком?
Конечно, ребята с легкостью справились с этой задачей. Таких букв 15.
Мы предположили, что буквы русского алфавита это графы. Может ключ к разгадке в количестве вершин, ребер, количестве четных и нечетных вершин графа?
Начнем с букв. Возьмем букву Б.
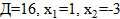
У нее 4 вершины, 4 ребра. Из вершины 1 выходит 1 ребро, из вершины 2 -2 ребра, из вершины 3- 3 ребра, из вершины 4 – 2 ребра. Получили 2 четные вершины и 2 нечетные вершины.
Таким образом, заполнили всю таблицу.
| Б | В | Г | З | И | Л | М | О | П | Р | С | Ф | Ъ | Ь | Я | |
| Кол-во вершин | 4 | 3 | 3 | 3 | 4 | 4 | 5 | 2 | 4 | 3 | 2 | 3 | 4 | 3 | 4 |
| Кол-во четных вершин | 2 | 3 | 1 | 1 | 2 | 2 | 3 | 2 | 2 | 1 | 0 | 1 | 2 | 1 | 2 |
| Кол-во нечетных вершин | 2 | 0 | 2 | 2 | 2 | 2 | 2 | 0 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Кол-во ребер | 4 | 4 | 2 | 2 | 3 | 3 | 4 | 3 | 3 | 1 | 4 | 4 | 3 | 4 | |
| Кол-во росчерков | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Что же мы заметили?
Если количество нечетных вершин равно 0 или 2, то можно одним росчерком начертить граф. Если только четные вершины (в данном случае буквы В и О) также можно не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии начертить граф. Количество четных вершин может быть четным и нечетным.
У нас возникли вопросы:
- если нечетных вершин не 2, а больше 2?
- зависит ли решение нашей задачи от количества четных и нечетных вершин?
Проверим эту гипотезу.
1. Начертим граф с нечетными вершинами (6 мостов).
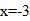
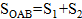
| Кол-во вершин | Кол-во четных вершин | Кол-во нечетных вершин |
| 4 | 0 | 4 |
Обойти все мосты не смогли.
В задаче о кенигсбергских мостах также все вершины нечетные.
Мы пришли к выводу: если все вершины нечетные, то обойти все мосты невозможно.
2. Начертим граф только с четными вершинами (9 мостов)
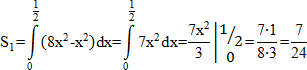
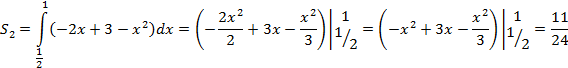
| Кол-во вершин | Кол-во четных вершин | Кол-во нечетных вершин |
| 5 | 5 | 0 |
В этом случае можно одним росчерком начертить граф.
Маршрут движения: САЕАВЕДВСД или наоборот. Что мы заметили?
Вывод: Если все вершины графа четные, то можно одним росчерком начертить граф.
3. Начертим граф, где имеются четные и нечетные вершины.
Пусть 9 мостов.
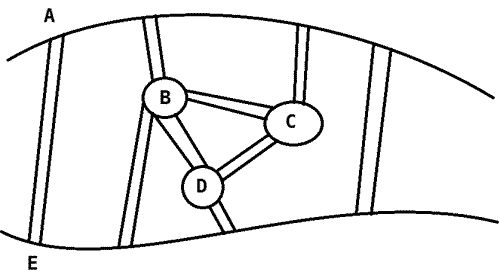
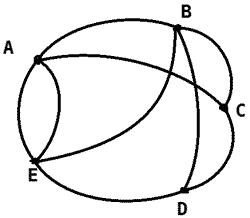
| Кол-во вершин | Кол-во четных вершин | Кол-во нечетных вершин |
| 5 | 3 | 2 |
В данном случае нечетных вершин 2.
В этом случае можно одним росчерком начертить граф.
Маршрут движения: САЕАВЕДВСД или наоборот. Что я заметил? Вершины С и Д нечетные.
Если мостов 14?
Из точки А выходят 4 моста, из В- 3 моста, С- 5 мостов, Д- 6 мостов, Е – 6 мостов, F – 4 моста. Две вершины В и С нечетные, а остальные вершины четные.
| Кол-во вершин | Кол-во четных вершин | Кол-во нечетных вершин |
| 6 | 4 | 2 |
Маршрут движения: ВАЕСДАСВДЕFДЕFС и наоборот.
Во всех этих двух случаях (для 9, 14 мостов) движение начинали от одной нечетной вершины и заканчивали на другой нечетной вершине. Количество четных вершин не имел значения, а количество нечетных вершин равно 2.
К чему мы пришли?
- Если все вершины графа четные, то можно одним росчерком начертить граф. При этом движение можно начать с любой вершины и окончить в той же вершине;
- если две вершины графа нечетные, то можно начертить одним росчерком. Движение надо начинать от любой нечетной вершины, а заканчивать на другой нечетной вершине;
- если более двух нечетных вершин, то невозможно начертить одним росчерком.
Еще мы обнаружили, что
- число нечетных вершин графа всегда четное;
- если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф, равно половине числа нечетных вершин этого графа.
4.12.2015
