Готовимся к олимпиаде

Категория: Математика.

Задание 1. Решите уравнение .

Решение. Один из возможных способов решения данного уравнения является введение параметра. Пусть , тогда уравнение примет вид:

.

Заметим, что оно является квадратным относительно а. Перепишем его в виде: .

Его дискриминант равен .

Тогда ; .

Значит исходное уравнение равносильно совокупности двух уравнений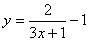

Ответ: .

Задание 2. Числа таковы что . Докажите, что .

Доказательство. Оценим каждый из множителей, применяя неравенство Коши: ; ; …, .

Умножив последние n неравенств получим: (т.к. ).

Неравенство доказано.

Задание 3. Решите уравнение .

Решение. ОДЗ уравнения .

Используя неравенство Коши имеем: ; ; ; ; .

Сложив последние неравенства получим: .

Тогда: 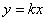. Последняя система решений не имеет.

Ответ: корней нет.

Задание 4. Найти все целые положительные числа x и y, что четырехзначное число — есть точный квадрат числа r, делящегося на 6.

Решение. ; . Тогда . Значит и .

Так как , то . Из чисел на 4 делятся только числа 92 и 96, но — точный квадрат, а значит не может оканчиваться цифрой 2. Значит остается только вариант . Тогда . Так как это число кратно 9, то или . Учитывая, что x — цифра, получим .

Ответ: , .

Задание 5. Найти отрезок, концы которого лежат на графике функции , а ось ординат для него является серединным перпендикуляром.

Решение. Поскольку ось ординат для искомого отрезка является серединным перпендикуляром, то , где и — абсциссы концов этого отрезка. Тогда

.

Значит: .

Ответ: координаты концов искомого отрезка и .

Задание 6. Решите уравнение .

Решение. Рассмотрим функцию . . — четная.

.

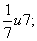Данная производная существует для любого x из области определения данной функции.

при .

при .

при .

Значит функция возрастает при и при , убывает и при .

— точка максимума,

— точки минимума.

— наименьшее значение функции .

И так как , то исходное уравнение равносильно системе: .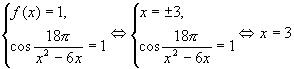

Ответ: 3.

Задание 7. При каких а система 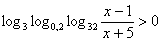имеет единственное решение?

Решение. Рассмотрим второе уравнение системы: .

Последнее уравнение — однородное второй степени. Пара является его решением, поэтому оно равносильно совокупности: или .

Дискриминант последнего уравнения: , так как .

Значит исходная система уравнений равносильна следующей системе уравнений:

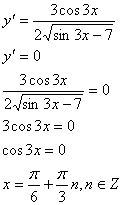
Ответ: 2.

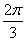Задание 8. Среди пар для каждой из которых система имеет единственное решение, выбрать ту, для которой выражение имеет наибольшее значение.

Решение.

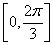
Если и одновременно, то последняя система имеет бесконечное множество решений — что не удовлетворяет условию.

Если и , то последняя система не имеет решений, что также не удовлетворяет условию задачи.

Значит , уравнение — квадратное. Поделив уравнение на , получим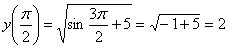

Чтоб последняя система имела единственное решение, дискриминант квадратного уравнения должен быть равен нулю.

; .

Значит пары , при которых достигается единственность решения системы имеет вид 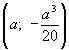, причем, по условию, . Найдем ту из них, чтобы выражение принимало наибольшее значение: .

Рассмотрим , при .

. существует для любого .

при ; .

при ; при .

— точка максимума.

Поскольку — единственная точка максимума при , то в ней достигает своего наибольшего значения.

.

Ответ: .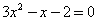

Задание 9. Решите уравнение .

Решение. Исходное уравнение равносильно следующему: .

Заметим, что уравнение имеет вид: , где .

. для любого.

Значит монотонна. Поэтому уравнение .

Ответ: .

Задание 10. Назовем числа “приблизительно равными”, если их (сумма) разность не больше 1. Сколько существует способов представить число 2004 в виде суммы целых положительных “приблизительно равных” слагаемых?

Решение. Пусть число 2004 разбито на k таких слагаемых. Пусть среди них S равны n и r равных . Тогда ; . Значит .

Ответ: 2003.

23.12.2005

• Назад
• Вперед